Introduction to Neural Networks
~ by @raphaelmcobe ~
Neural Networks
- Neurons as structural constituents of the brain [Ramón y Cajál, 1911];
- Five to six orders of magnitude slower than silicon logic gates;
- In a silicon chip happen in the nanosecond (on chip) vs millisecond range (neural events);
- A truly staggering number of neurons (nerve cells) with massive interconnections between them;
Neural Networks
- Receive input from other units and decides whether or not to fire;
- Approximately 10 billion neurons in the human cortex, and 60 trillion synapses or connections [Shepherd and Koch, 1990];
- Energy efficiency of the brain is approximately $10^{−16}$ joules per operation per second against ~ $10^{−8}$ in a computer;
Neurons
Neurons
- input signals from its dendrites;
- output signals along its (single) axon;
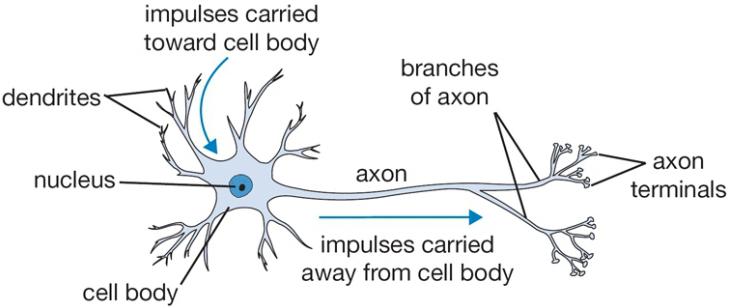
Neurons
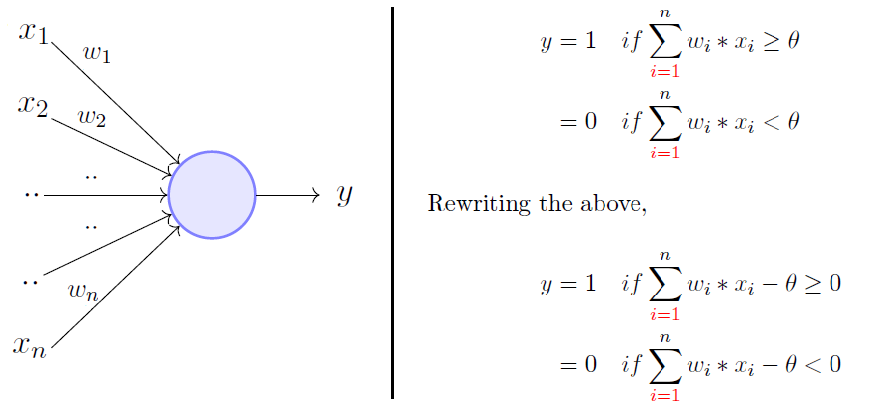
How do they work?
- Control the influence from one neuron on another:
- Excitatory when weight is positive; or
- Inhibitory when weight is negative;
- Nucleus is responsible for summing the incoming signals;
- If the sum is above some threshold, then fire!
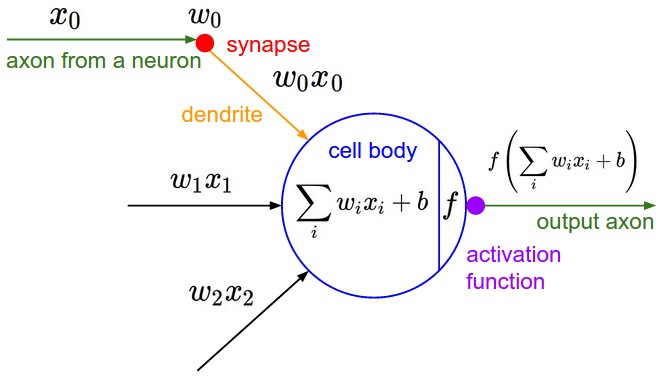
Neurons
Artificial Neuron
Neural Networks
Neural Networks
- It appears that one reason why the human brain is so powerful is the sheer complexity of connections between neurons;
- The brain exhibits huge degree of parallelism;
Artificial Neural Networks
- Model each part of the neuron and interactions;
- Interact multiplicatively (e.g. $w_0x_0$) with the dendrites of the other neuron based on the synaptic strength at that synapse (e.g. $w_0$ );
- Learn synapses strengths;
Artificial Neural Networks
Function Approximation Machines
- Datasets as composite functions: $y=f^{*}(x)$
- Maps $x$ input to a category (or a value) $y$;
- Learn synapses weights and aproximate $y$ with $\hat{y}$:
- $\hat{y} = f(x;w)$
- Learn the $w$ parameters;
Artificial Neural Networks
- Can be seen as a directed graph with units (or neurons) situated at the vertices;
- Some are input units
- Receive signal from the outside world;
- The remaining are named computation units;
- Each unit produces an output
- Transmitted to other units along the arcs of the directed graph;
Artificial Neural Networks
- Input, Output, and Hidden layers;
- Hidden as in “not defined by the output”;
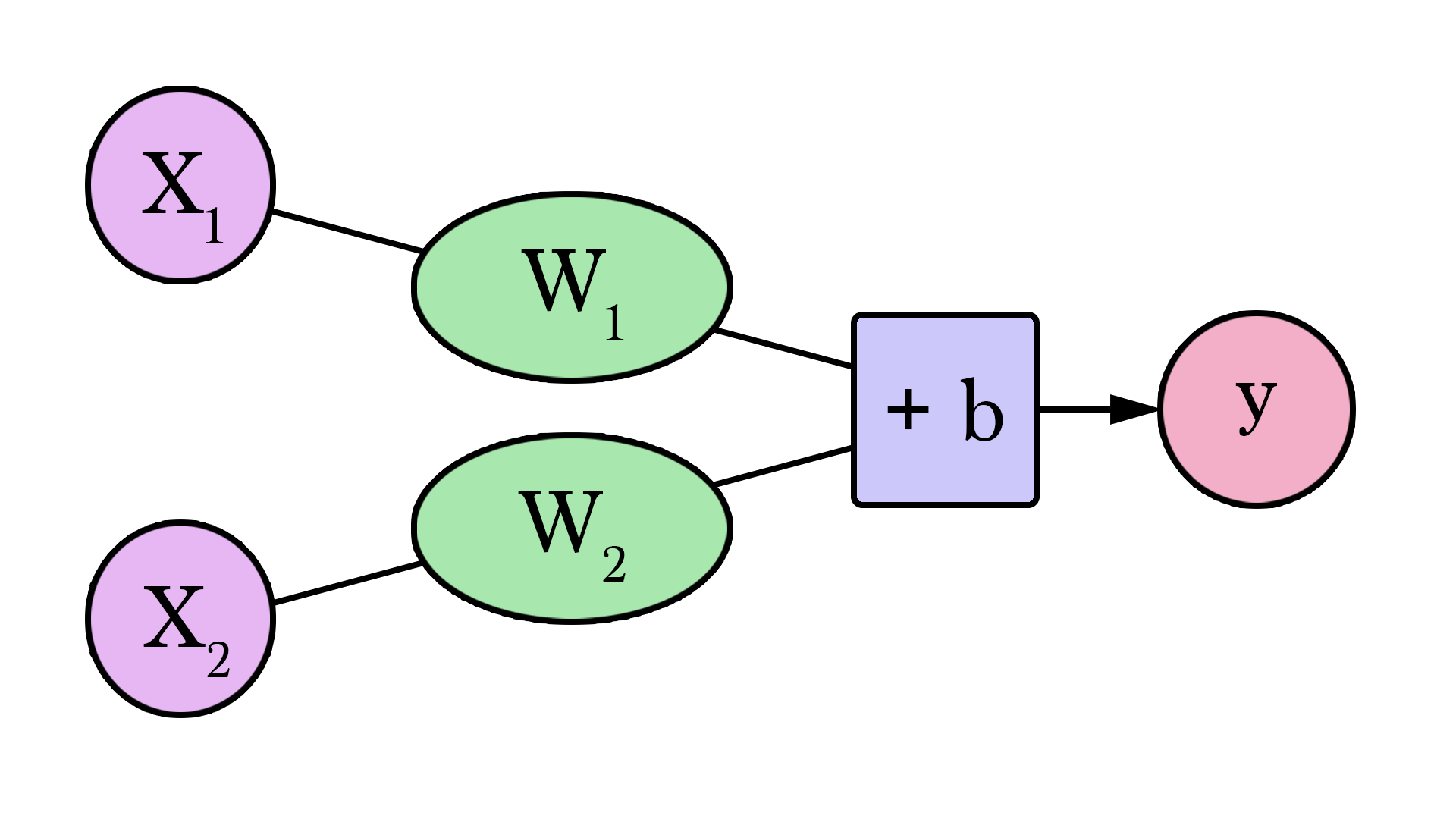
Artificial Neural Networks
Motivation Example (taken from Jay Alammar blog post)
- Imagine that you want to forecast the price of houses at your neighborhood;
- After some research you found that 3 people sold houses for the following values:
| Area (sq ft) (x) | Price (y) |
|---|---|
| 2,104 | $\$399,900$ |
| 1,600 | $\$329,900$ |
| 2,400 | $\$369,000$ |
Artificial Neural Networks
Motivation Example (taken from Jay Alammar blog post)
If you want to sell a 2K sq ft house, how much should ask for it?
How about finding the average price per square feet?
$\$180$ per sq ft.
Artificial Neural Networks
Motivation Example (taken from Jay Alammar blog post)
- Our very first neural network looks like this:
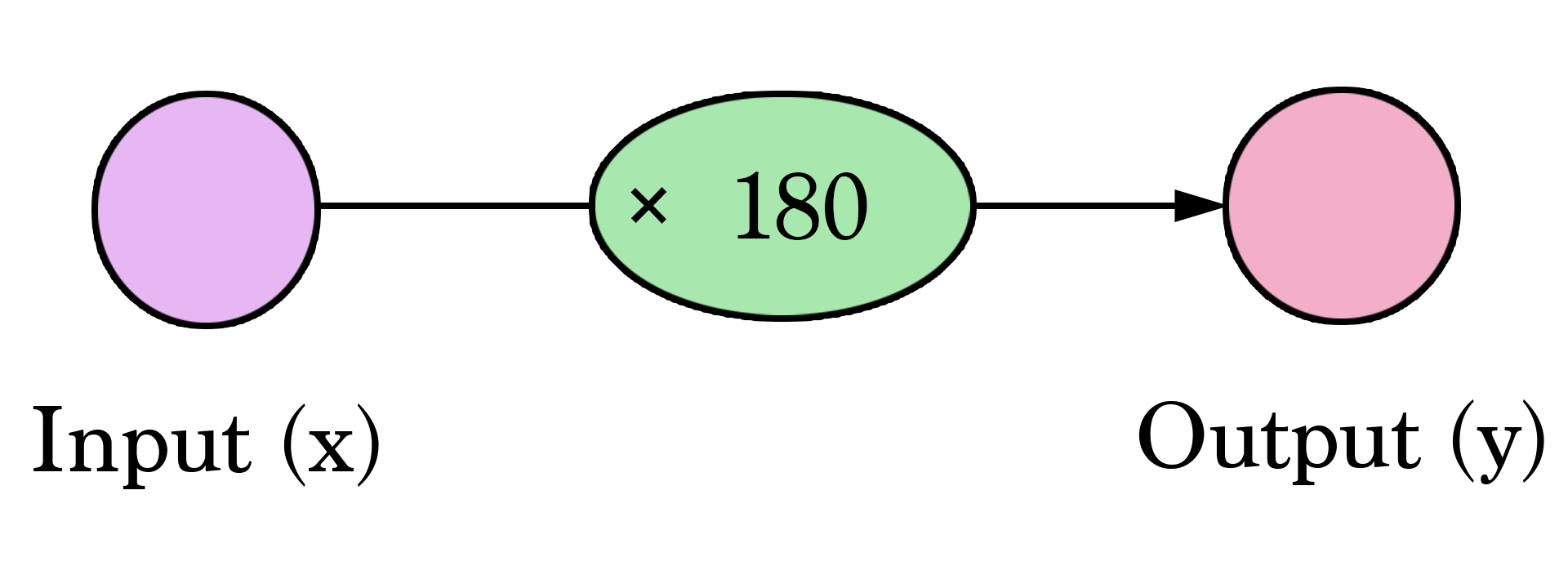
Artificial Neural Networks
Motivation Example (taken from Jay Alammar blog post)
- Multiplying $2,000$ sq ft by $180$ gives us $\$360,000$.
- Calculating the prediction is simple multiplication.
- We needed to think about the weight we’ll be multiplying by.
- That is what training means!
| Area (sq ft) (x) | Price (y) | Estimated Price($\hat{y}$) |
|---|---|---|
| 2,104 | $\$399,900$ | $\$378,720$ |
| 1,600 | $\$329,900$ | $\$288,000$ |
| 2,400 | $\$369,000$ | $\$432,000$ |
Artificial Neural Networks
Motivation Example (taken from Jay Alammar blog post)
- How bad is our model?
- Calculate the Error;
- A better model is one that has less error;
Mean Square Error : $2,058$
| Area (sq ft) (x) | Price (y) | Estimated Price($\hat{y}$) | $y-\hat{y}$ | $(y-\hat{y})^2$ |
|---|---|---|---|---|
| 2,104 | $\$399,900$ | $\$378,720$ | $\$21$ | $449$ |
| 1,600 | $\$329,900$ | $\$288,000$ | $\$42$ | $1756$ |
| 2,400 | $\$369,000$ | $\$432,000$ | $\$-63$ | $3969$ |
Artificial Neural Networks
- Fitting the line to our data:
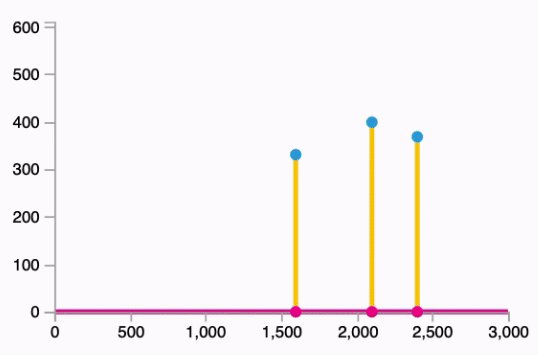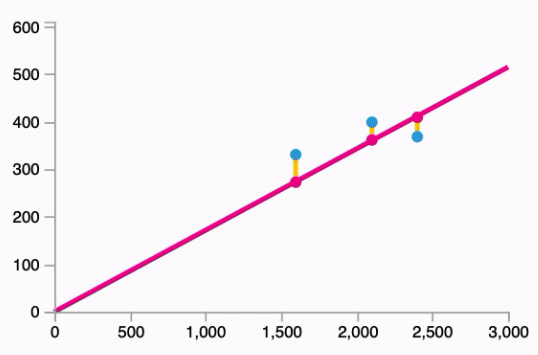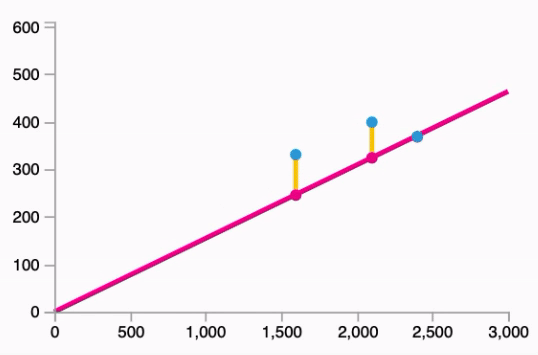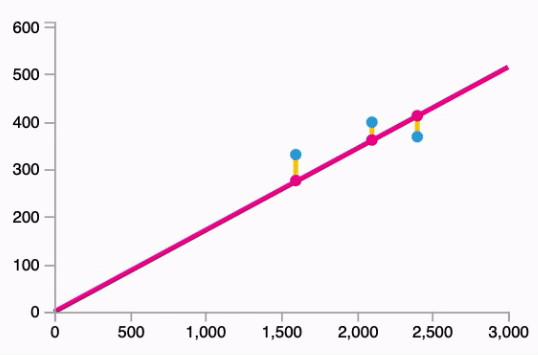
Follows the equation: $\hat{y} = W * x$
Artificial Neural Networks
How about addind the Intercept?
$\hat{y}=Wx + b$
Artificial Neural Networks
The Bias
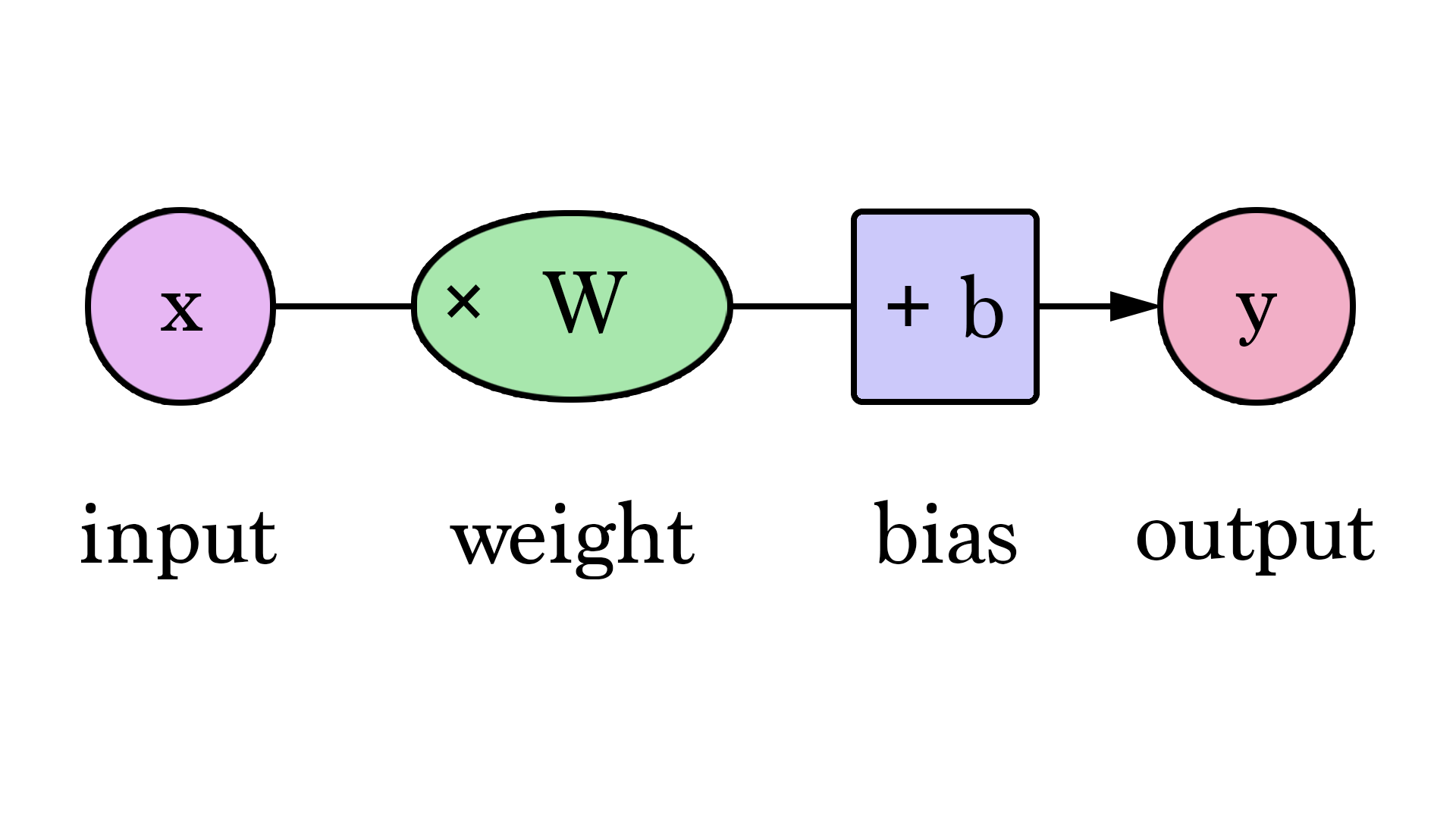
Artificial Neural Networks
Try to train it manually:
Artificial Neural Networks
How to discover the correct weights?
- Gradient Descent:
- Finding the minimum of a function;
- Look for the best weights values, minimizing the error;
- Takes steps proportional to the negative of the gradient of the function at the current point.
- Gradient is a vector that is tangent of a function and points in the direction of greatest increase of this function.
Artificial Neural Networks
Gradient Descent
- In mathematics, gradient is defined as partial derivative for every input variable of function;
- Negative gradient is a vector pointing at the greatest decrease of a function;
- Minimize a function by iteratively moving a little bit in the direction of negative gradient;
Artificial Neural Networks
Gradient Descent
- With a single weight:
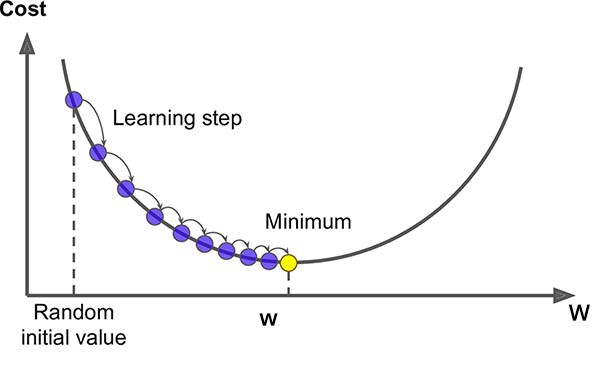
Artificial Neural Networks
Gradient Descent
Artificial Neural Networks
Perceptron
- In 1958, Frank Rosenblatt proposed an algorithm for training the perceptron.
- Simplest form of Neural Network;
- One unique neuron;
- Adjustable Synaptic weights
Artificial Neural Networks
Perceptron
- Classification of observations into two classes:
Images Taken from Towards Data Science
Artificial Neural Networks
Perceptron
- Classification of observations into two classes:
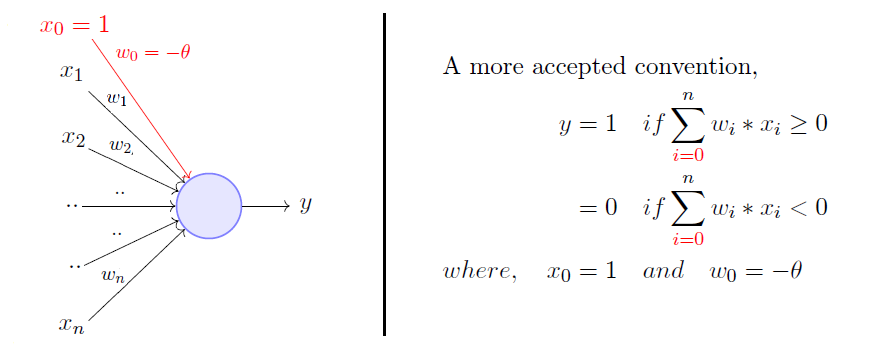
Images Taken from Towards Data Science
Artificial Neural Networks
Perceptron
- E.g, the OR function:

Find the $w_i$ values that could solve the or problem.
Artificial Neural Networks
Perceptron
- E.g, the OR function:
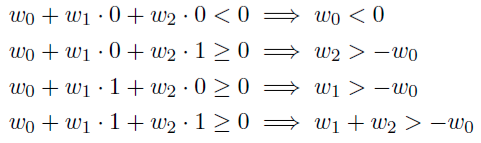
Artificial Neural Networks
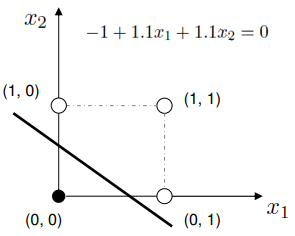
Perceptron
- One possible solution $w_0=-1$, $w_1=1.1$, $w_2=1.1$:
Artificial Neural Networks
The Keras framework
- High-level neural networks API;
- Capable of running on top of TensorFlow, CNTK, or Theano;
- Focus on enabling fast experimentation;
- Go from idea to result with the least possible delay;
- Runs seamlessly on CPU and GPU;
- Compatible with: Python 2.7-3.6;
Artificial Neural Networks
The Keras framework
Use the implementation of the tensorflow:
Create a sequential model (perceptron)
# Import the Sequential model from tensorflow.keras.models import Sequential # Instantiate the model model = Sequential()
Artificial Neural Networks
The Keras framework
Create a single layer with a single neuron:
unitsrepresent the number of neurons;# Import the Dense layer from tensorflow.keras.layers import Dense # Add a forward layer to the model model.add(Dense(units=1, input_dim=2))
Artificial Neural Networks
The Keras framework
Compile and train the model
The compilation creates a computational graph of the training;
# Specify the loss function (error) and the optimizer # (a variation of the gradient descent method) model.compile(loss="mean_squared_error", optimizer="sgd") # Fit the model using the train data and also # provide the expected result model.fit(x=train_data_X, y=train_data_Y)
Artificial Neural Networks
The Keras framework
Evaluate the quality of the model:
# Use evaluate function to get the loss and other metrics that the framework # makes available loss_and_metrics = model.evaluate(train_data_X, train_data_Y) print(loss_and_metrics) #0.4043288230895996 # Do a prediction using the trained model prediction = model.predict(train_data_X) print(prediction) # [[-0.25007164] # [ 0.24998784] # [ 0.24999022] # [ 0.7500497 ]]
Artificial Neural Networks
The Keras framework
Exercise:
Run the example of the Jupyter notebook:
Perceptron - OR
Artificial Neural Networks
Perceptron
Exercise:
- What about the AND function?
| $x_1$ | $x_2$ | $y$ |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Artificial Neural Networks
Activation Functions
- Describes whether or not the neuron fires, i.e., if it forwards its value for the next neuron layer;
Historically they translated the output of the neuron into either 1 (On/active) or 0 (Off) - Step Function:
if prediction[i]>0.5: return 1 return 0
Artificial Neural Networks
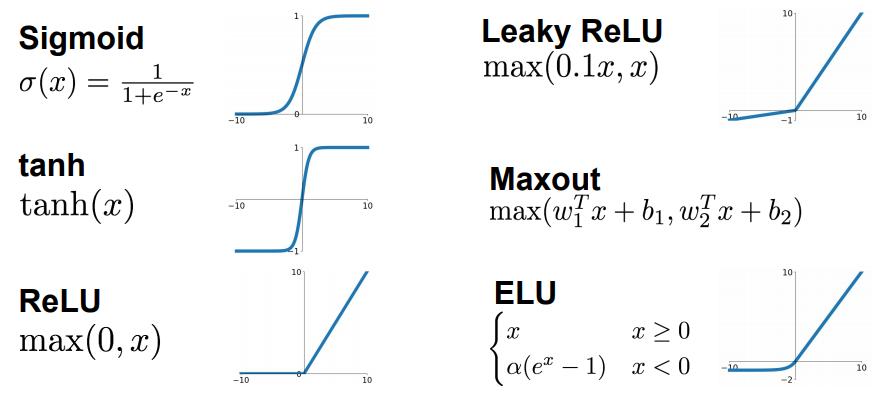
Activation Functions
- Multiply the input by its weights, add the bias and applies activation;
- Sigmoid, Hyperbolic Tangent, Rectified Linear Unit;
- Differentiable function instead of the step function;
Artificial Neural Networks
The Bias
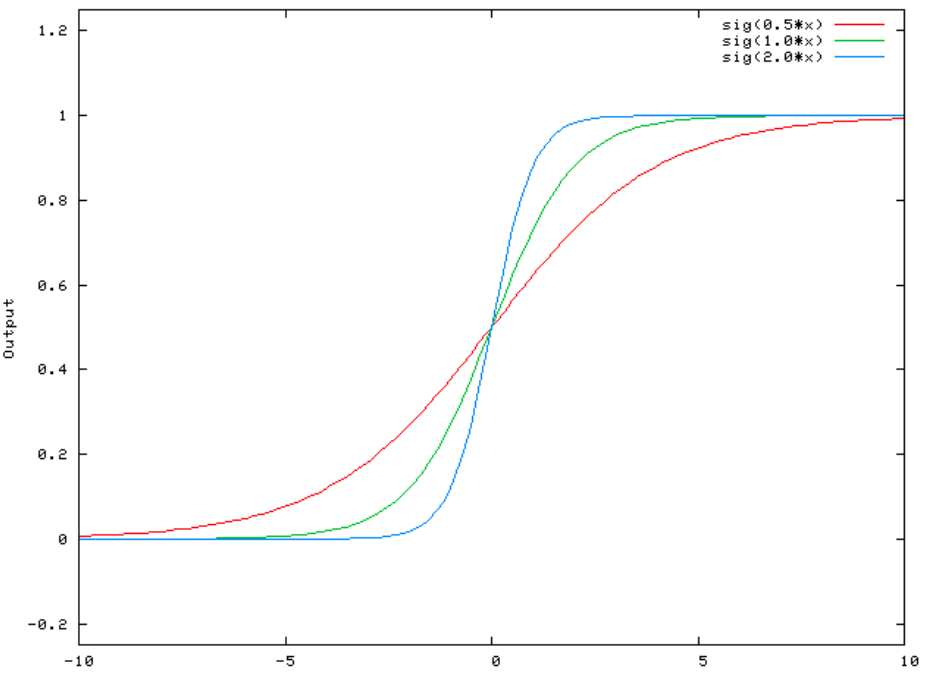
Artificial Neural Networks
The Bias
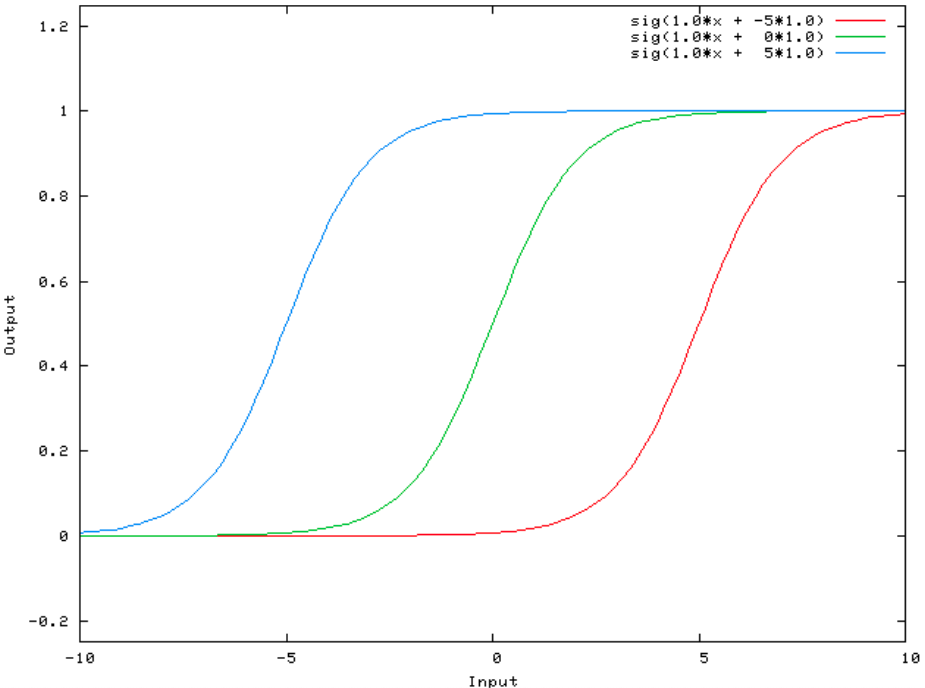
Artificial Neural Networks
Perceptron - What it can’t do!
- The XOR function:
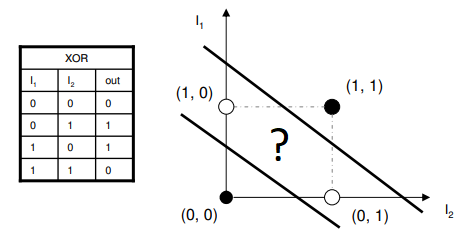
Artificial Neural Networks
Perceptron - Solving the XOR problem
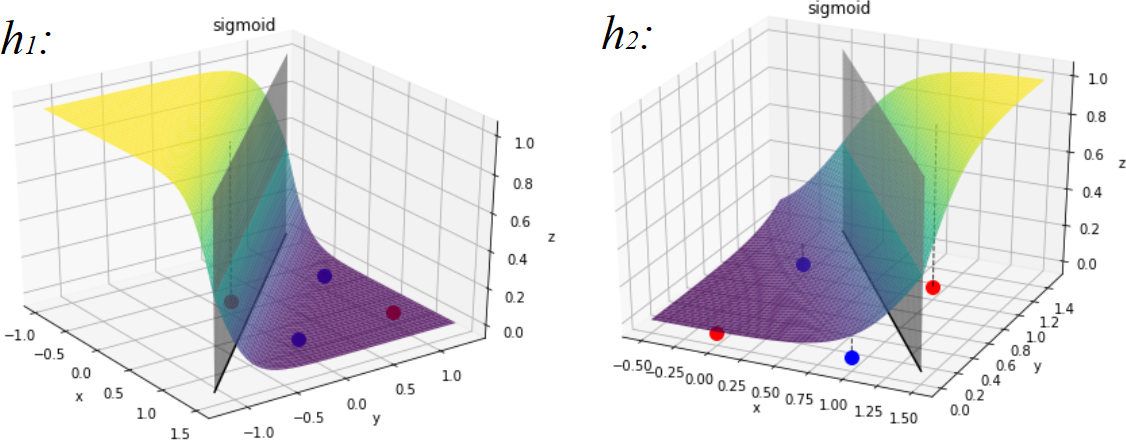
- 3D example of the solution of learning the OR function:
- Using Sigmoid function;
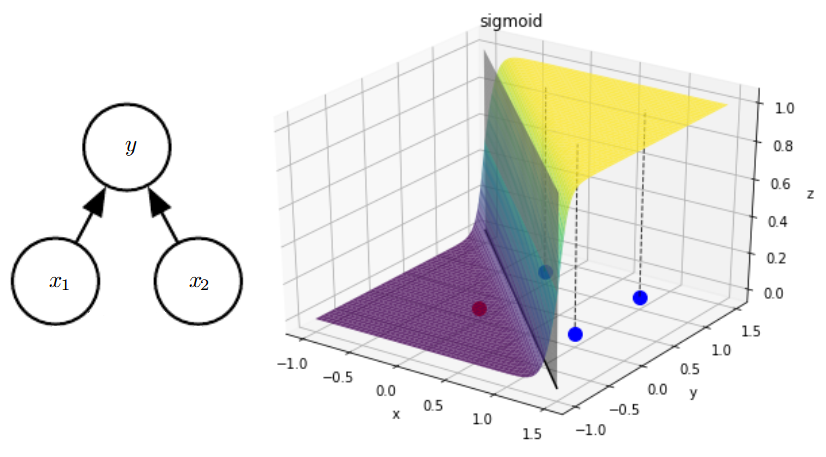
- Using Sigmoid function;
Artificial Neural Networks
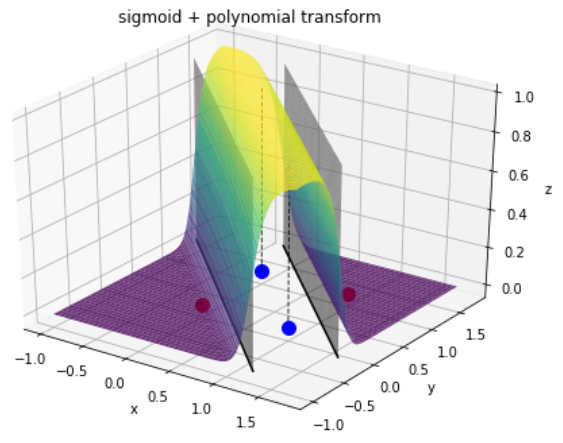
Perceptron - Solving the XOR problem
Artificial Neural Networks
Perceptron - Solving the XOR problem
Artificial Neural Networks
Perceptron - Solving the XOR problem
Implementing an ANN that can solve the XOR problem:
Add a new layer with a larger number of neurons:
... #Create a layer with 4 neurons as output model.add(Dense(units=4), activation="sigmoid", input_dim=2) # Connect to the first layer that we defined model.add(Dense(units=1, activation="sigmoid")
Artificial Neural Networks
Multilayer Perceptrons - Increasing the model power
Typically represented by composing many different functions: $$y = f^{(3)}(f^{(2)}(f^{(1)}(x)))$$
The depth of the network - the deep in deep learning! (-;
Artificial Neural Networks
Multilayer Perceptrons - Increasing the model power
- Information flows from $x$ , through computations and finally to $y$.
- No feedback!
Artificial Neural Networks
Understanding the training
Plot the architecture of the network:
tf.keras.utils.plot_model(model, show_shapes=True, show_layer_names=False)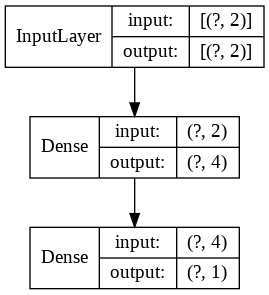
Artificial Neural Networks
Understanding the training
Plotting the training progress of the XOR ANN:
history = model.fit(x=X_data, y=Y_data, epochs=2500, verbose=0) import matplotlib.pyplot as plt plt.plot(history.history['loss']) plt.title('Model Training Progression') plt.ylabel('Loss') plt.xlabel('Epoch') plt.legend(['Loss'], loc='upper left') plt.show()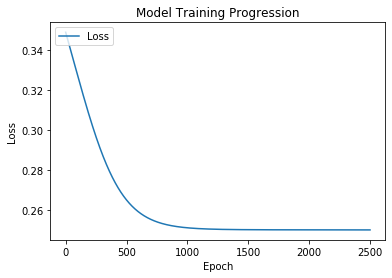
Artificial Neural Networks
Problems with the training procedure:
Artificial Neural Networks
Optimization alternatives
- The Gradient Descent is not always the best option to go with:
- Only does the update after calculating the derivative for the whole dataset;
- Can take a long time to find the minimum point;
Artificial Neural Networks
Optimization alternatives
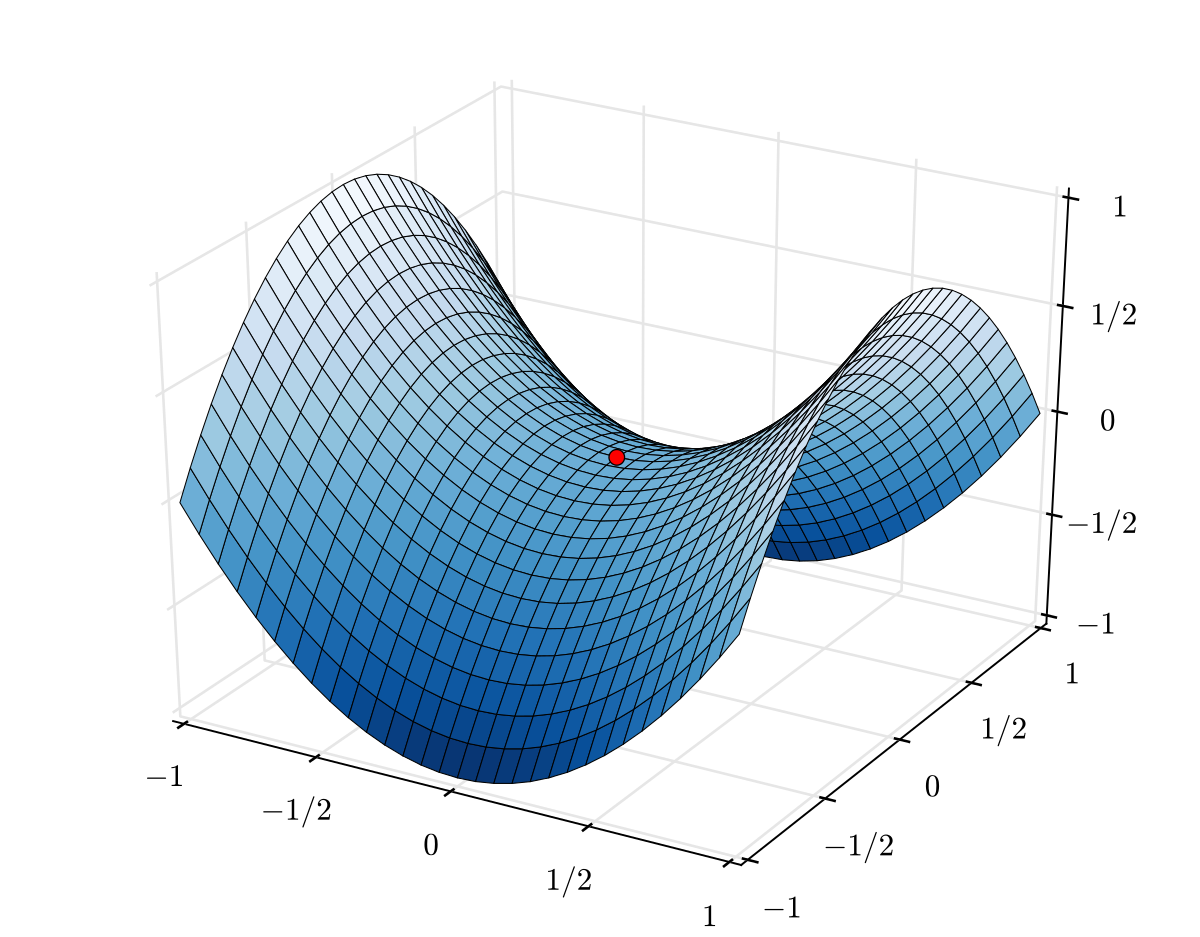
- The Gradient Descent is not always the best option to go with:
- For non-convex surfaces, it may only find the local minimums - the saddle situation;
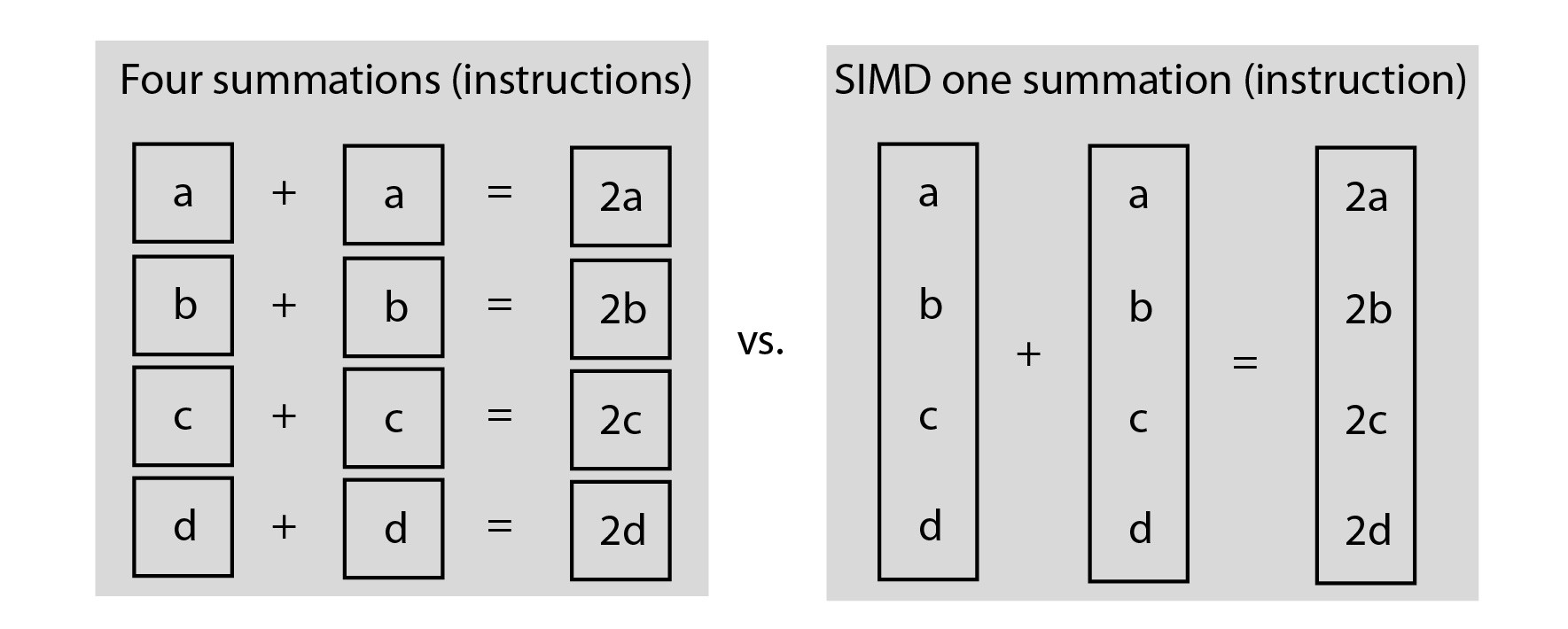
- Vectorization
Artificial Neural Networks
Optimization alternatives
Gradient Descent alternatives:
- Stochastic Gradient Descent: updates at each input;
Minibatch Gradient Descent: updates after reading a batch of examples;
Animations taken from Vikashraj Luhaniwal post.
Artificial Neural Networks
Optimization alternatives
Adaptative Learning Rates:
Artificial Neural Networks
Multilayer Perceptron - XOR
Try another optimizer:
model.compile(loss="mean_squared_error", optimizer="adam")My solution
Artificial Neural Networks
Predicting probabilities
Artificial Neural Networks
Predicting probabilities
- The Softmax function;
- Takes an array and outputs a probability distribution, i.e., the probability of the input example belonging to each of the classes in my problem;
One of the activation functions available at
Keras:model.add(Dense(2, activation="softmax"))
Artificial Neural Networks
Loss functions
- For regression problems
- Mean squared error is not always the best one to go;
- What if we have a three classes problem?
- Alternatives:
mean_absolute_error,mean_squared_logarithmic_error
Artificial Neural Networks
Loss functions
- Cross Entropy loss:
- Default loss function to use for binary classification problems.
- Measures the performance of a model whose output is a probability value between 0 and 1;
- Loss increases as the predicted probability diverges from the actual label;
- A perfect model would have a log loss of 0;
Artificial Neural Networks
Dealing with overfitting
- Dropout layers:
- Randomly disable some of the neurons during the training passes;
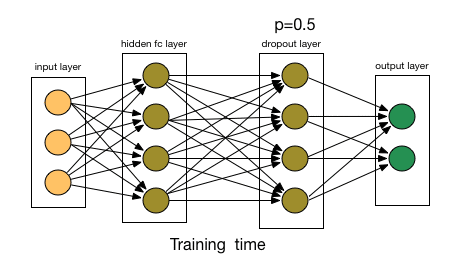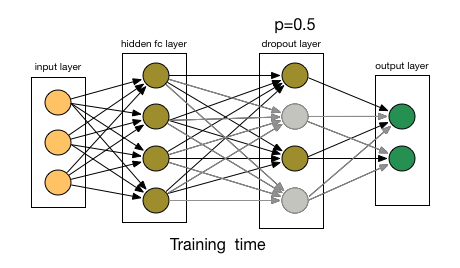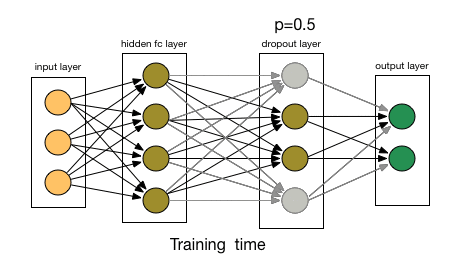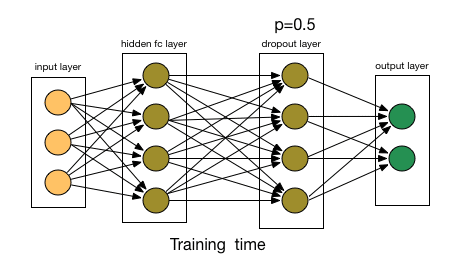
Artificial Neural Networks
Dealing with overfitting
Dropout layers:
# Drop half of the neurons outputs from the previous layer model.add(Dropout(0.5))
Artificial Neural Networks
Larger Example
- The MNIST dataset: database of handwritten digits;
- Dataset included in Keras;

Artificial Neural Networks
The MNIST MLP
- Try to improve the classification results using this notebook:
- Things to try:
- Increase the number of neurons at the first layer;
- Change the optimizer and the loss function;
- Try
categorical_crossentropyandrmspropoptimizer; - Try adding some extra layers;
Artificial Neural Networks
The MNIST MLP
- Try to improve the classification results using this notebook:
Things to try:
- Try addind
Dropoutlayers; - Increase the number of
epochs; - Try to normalize the data!
- Try addind
What is the best accuracy?
The Exercise
Artificial Neural Networks
The Exercise
Artificial Neural Networks
The Exercise
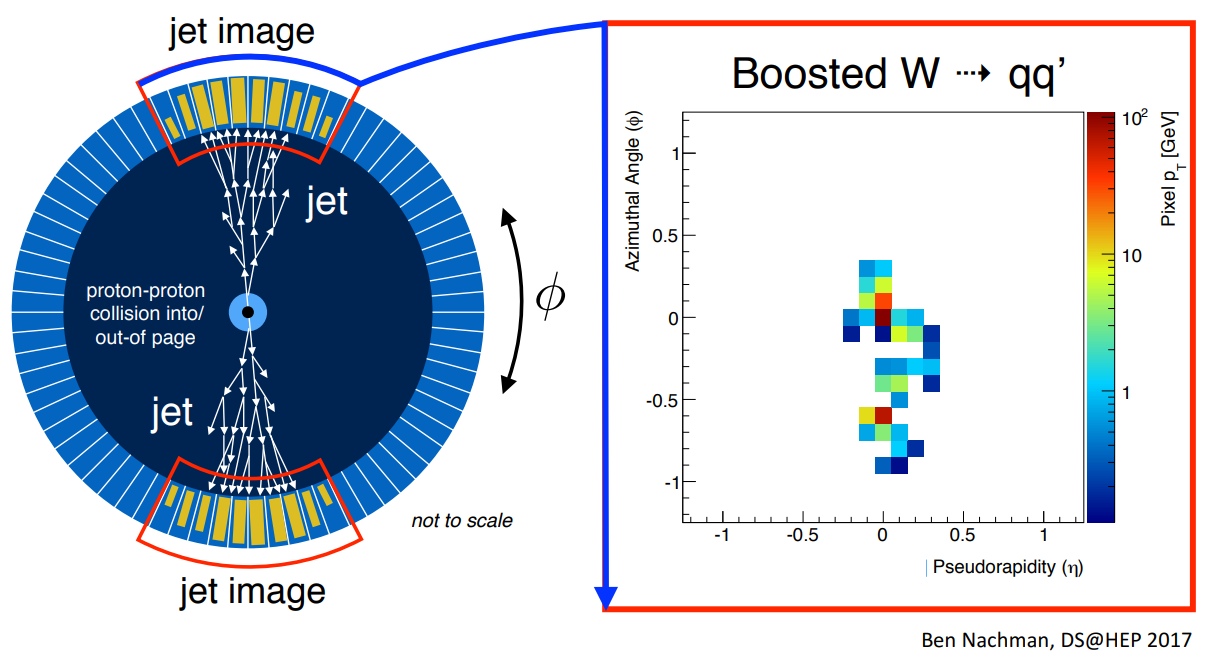
Artificial Neural Networks
The Exercise
Artificial Neural Networks
Signal VS Background
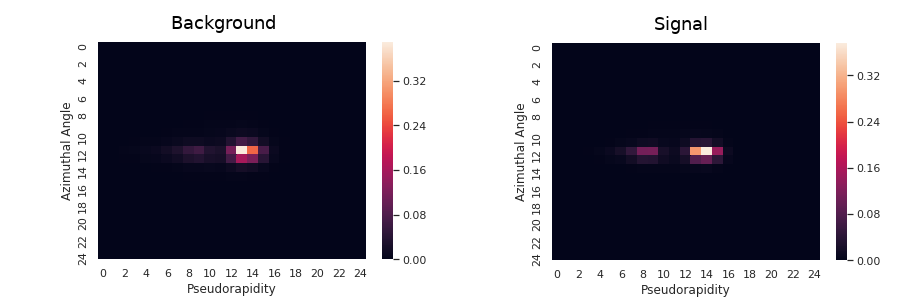
Artificial Neural Networks
Signal VS Background
Run this Jupyter Notebook for performing the Jet Classification.